See the guide for this topic.
4.1 – Oscillations
-
Simple harmonic oscillations
Oscillations are periodic motions which center around an equilibrium position.
Simple harmonic motion (SHM) is a special type of oscillation. For example:
- The simple pendulum
- The vibration of strings in a violin
- The spring-mass system, where the mass is initially displaced to produce a periodic motion around the equilibrium position
An object undergoes SHM if it experiences a force which is proportional and opposite of the displacement from its equilibrium position.
The period is independent of the amplitude of the SHM and can be given by the following equation
for a pendulum
and

for a spring-mass system
-
Time period, frequency, amplitude, displacement and phase difference
| Displacement (x) | Amplitude | Period (T) | Frequency (f) | Phase difference |
| Displacement of the oscillating object at a specific time from its equilibrium position | Maximum displacement of the oscillating object | Time taken for one complete oscillation (in seconds) | Number of times the object oscillates per unit time (usually one second)
f=1/T |
The difference between two SHMs with the same frequency in terms of their relative position in a cycle measured in radian |

-
Conditions for simple harmonic motion
- When the body is displaced from equilibrium, there must exist a restoring force (a force that wants to pull the body back to equilibrium).
- The magnitude of the restoring force must be proportional to the displacement of the body and acts towards the equilibrium.
4.2 – Travelling waves
-
Travelling waves
A travelling wave is a continuous disturbance in a medium characterized by repeating oscillations. For example:
- A rope that is flicked up and down continuously creates a repeating disturbance similar to the shape of a sine/cosine wave.
Energy is transferred by waves.
Matter is not transferred by waves.
The direction of a wave is defined by the direction of the energy transfer.
-
Wavelength, frequency, period and wave speed

Wavelength, frequency, and period follow the same rules of SHM.
Wave speed can be calculated by the following equation

-
Transverse and longitudinal waves
| Transverse wave | Longitudinal wave |
The direction of oscillation is perpendicular to the direction of the wave
|
The direction of oscillation is parallel to the direction of the wave |
| Example:
Water waves Wave in a string flicked up and down Light (electromagnetic waves) |
Example:
Wave produced in a spring Sound waves Earthquake P-waves |
FYI
| Transverse wave | Longitudinal wave |
| A point with maximum positive displacement is called a crest.
A point with minimum displacement is called a trough. |
A region where particles are closed to each other is called a compression.
A region where particles are furthest apart from each other is called a rarefaction. |
 |
 |
-
The nature of electromagnetic waves
All EM waves travel in vacuum at the same speed of 3*10^8m/s.
EM waves are transverse waves.

-
The nature of sound waves
The speed of sound in 20 degrees Celsius dry air is approximately 343.2m/s.
Sound waves are longitudinal waves.

4.3 – Wave characteristics
-
Wavefronts and rays
Wavefronts:
- Lines joining points which vibrate in phase.
- Can be straight lines or curves.
- The distance between successive wavefronts is the wavelength of the wave.
Rays:
- Lines which indicate the direction of wave propagation.
- Rays are perpendicular to wavefronts.

-
Amplitude and intensity
The amplitude and intensity of a wave depends on its energy.
The intensity of a wave is proportional to the square of its amplitude (I∝A^2).

-
Transverse and longitudinal waves
See previous section with the same title.
-
Superposition
The principle of superposition states that the net displacement of the underlying medium for a wave is equal to the sum of the individual wave displacements.

The left shows constructive interference (superposition) where the two waves add up (e.g. 1+1=2). The right shows deconstructive interference (superposition) where the two waves cancel each other (e.g. 1+(-1)=0).
-
Polarization
Light is a transverse wave (polarization only occur to transverse waves).
The polarization of light refers to the orientation of the oscillation in the underlying electric field.
Light is plane polarized if the electric field oscillates in one plane.

Left shows unpolarized light and right shows polarized light.
Polarization by reflection
When light is transmitted across a boundary between two mediums with different refractive indexes, part of the light is reflected and the remaining part is refracted (for further explanation, see section 4.4).
The light reflected is partially polarized, meaning that it is a mixture of polarized light and unpolarized light.
The extent to which the reflected light is polarized depends on the angle of incidence and the refractive index of the two mediums.
The angle of incidence at which the reflected light is totally polarized is called the Brewster’s angle (ϕ) given by the equation

where n1 and n2 are the refractive indexes for their respective mediums
When the angle of incidence is equal to Brewster’s angle, the reflected ray is totally polarized and the reflected ray is perpendicular to the refracted ray.

Polarizers and Analyzers
Polarizer:
- A polarizer is a sheet of material which polarizes light.
- When unpolarized light passes through a polarizer, its intensity is reduced by 50%.
Analyzer:
- When polarized light passes through a polarizer, its intensity will be reduced by a factor dependent on the orientation of the polarizer. This property allows us to deduce the polarization of light by using a polarizer.
- A polarizer used for this purpose is called an analyzer.
Malus’ Law relates the incident intensity and transmitted intensity of light passing through a polarizer and an analyzer.

where I is the transmitted intensity, I0 is the initial light intensity upon the analyzer, θ is the angle between the transmission axis and the analyzer.


When light passes through an optically active substance, the plane of polarization rotates.
4.4 – Wave behaviour
-
Reflection and refraction
Reflection

Angle of incidence = Angle of reflection
Reflection of waves from a fixed end is inverted.

Reflection of waves from a free end is not inverted.

Refraction
Refraction is the change in direction of a wave when it transmits from one medium to another.

The angle of incidence and the angle of refraction can be determined by Snell’s law given by the following formula

where n1 and n2 are the refractive indexes for their respective mediums


Fast-to-slow: towards normal; slow-to-fast: away from normal
In addition, the refractive index n1 and n2 are related by the following equation

where v1 and v2 are the speed of the waves in their respective mediums and λ1 and λ2 are the wavelength of the waves of their respective mediums

-
Snell’s law, critical angle and total internal reflection
See previous section (Reflection and refraction) for Snell’s law.

The refractive index and the critical angle are related by the following equation Total internal reflection only occurs when the light ray propagates from a optically denser medium to an optically less dense medium.
Total internal reflection only occurs when the light ray propagates from a optically denser medium to an optically less dense medium.
-
Diffraction through a single-slit and around objects
- Diffraction through a single-slit

Single-slit equations are not required for the standard level course.
- Diffraction around objects

-
Interference patterns
Maximums form at constructive interference (the maximum is shown by 1-2) and minimums form at deconstructive interference (the first minimum is shown by 3-4).




-
Double-slit interference
Like single-slit diffraction, double-slit diffraction occurs via the same methods of interference and has a similar diffraction pattern.
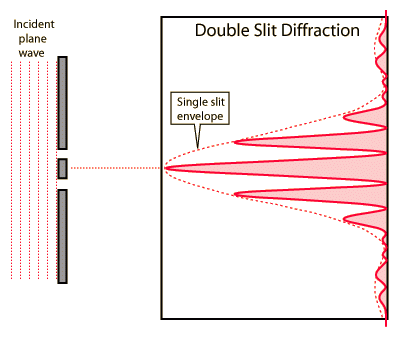

-
Path difference



4.5 – Standing waves
-
The nature of standing waves
Standing waves (stationary) waves result from the superposition of two opposite waves which are otherwise identical.
Energy is not transferred by standing waves.

A wave hits a wall and is reflected identically opposite.

The black wave shows the wave created by the superposition of the blue and green waves.

-
Boundary conditions
Air particles can oscillate and create standing waves in pipes with open or closed ends.
Antinodes are positioned at open ends and nodes are positioned at closed ends.
Standing waves on a string is equivalent to that in a pipe which is closed on both ends (nodes-node).

The following table summarizes the behavior of standing waves in pipes and strings:
| One closed end and one open end | Two closed ends | Two open ends |
 |
1st Harmonic
|
 |
 |
2nd Harmonic
|
 |
 |
3rd Harmonic
|
 |
| nth Harmonic
λ=4L/n (Note that even harmonics do not exist for pipes with one closed end and one open end) |
nth Harmonic
λ=2L/n |
nth Harmonic
λ=2L/n |
-
Nodes and antinodes
Positions along the wave which are fixed are called nodes (minimum) and those with the largest displacement are called antinodes (maximum).
For standing waves, the distance between adjacent nodes = the distance between adjacent antinodes = λ/2.

FYI
Difference between standing waves and travelling waves
| Standing waves | Travelling waves |
| No energy is propagated along a standing wave
A standing wave has nodes and antinodes The amplitude of the standing wave varies along the wave Particles between two adjacent nodes oscillate in phase and particles separated by exactly one node oscillate in antiphase. |
Energy is propagated in a travelling wave
A travelling wave has neither nodes nor antinodes The amplitude of the travelling wave is constant throughout the wave The phase difference between two particles of a travelling wave can take any value between 0 and 2π |